Factorial Designs: Introduction
Experimental psychologists select or manipulate one or more conditions in order to determine their effects on one or more measures of the behavior of a subject. For example, a researcher, Sally, may be interested in whether or not a particular drug impedes memory. She runs an experiment in which each session starts with a subject swallowing a pill. Sometimes the pill does not contain the drug (placebo), and other times the pill contains 10 mg of the drug. Subjects then complete a memory task, and their scores are noted.
The behavioral measure(s) is called the dependent variable. Test scores on the memory task would be the dependent variable because they are being used as a measure to assess the behavioral effect of the drug.
The manipulated condition(s) is called the independent variable. In our example, because Sally manipulates the presence or absence of the drug in the pill, drug dosage is considered to be the independent variable. Another name for the independent variable is factor. Let us refer to drug dosage as Factor A. Sally's experiment contains two values or levels of Factor A: 0 mg and 10 mg. Let us refer to the two levels of Factor A as A1 and A2, respectively.
This example illustrates the simplest design employed by experimental psychologists: one independent variable with two levels and one dependent variable. Many research problems, however, require more complex experimental designs. There are a number of possibilities. First, the experimenter may be interested in studying the effects of the independent variable on more than one dependent variable. For example, Sally may choose as her dependent variables: (1) memory as measured by test scores and (2) arousal as measured by heart rate. Perhaps she suspects that memory will be impeded by the drug because the drug elicits anxiety-like symptoms. Second, the experimenter may be interested in studying the effects of more than two levels (presence or absence) of the independent variable on the dependent variable. In our example, Sally may choose to administer three dosages of the drug: 0 mg (A1), 5 mg (A2), and 10 mg (A3). By including more than two levels of the independent variable the experimenter may discover a nonlinear relationship that would otherwise have gone unidentified (see Figure 1 below).
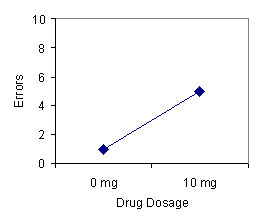
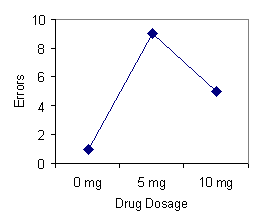
FIGURE 1. Errors as a function of the drug dosage in an experiment that used two levels of drug dosage (left panel) and in an experiment that used three levels of drug dosage (right panel).
A third possibility, and the topic of this section, is that the experimenter may be interested in studying the effects of several independent variables on the dependent variable. Returning to our original example with drug dosage as an independent variable with two levels, suppose Sally suspects her description of the task will influence the results. She therefore decides to manipulate this variable as well. Task description will be called Factor B. Sally varies two levels of Factor B: subjects are either told nothing about the task (B1) or they are told that the task is "hard" (B2).
In a factorial design "two or more variables, or factors, are employed in such a way that all the possible combinations of selected values of each variable are used (McBurney, 2004, p. 286). Each combination constitutes a condition. Were Sally to employ a factorial design, her experiment would need to include four conditions: no drug and no task description (A1B1); no drug and "hard task" description (A1B2); (3) drug and no task description (A2B1); and (4) drug and "hard task" description (A2B2). Tables are helpful in conceptualizing factorial designs. Sally's experiment is outlined in Table 1 below.
| TASK DESCRIPTION (B) | |||||||
| None (B1) | "Hard" (B2) | ||||||
| DRUG DOSAGE (A) | 0 mg (A1) |
|
|||||
| 10 mg (A2) | |||||||
This experiment is an example of a 2 x 2 factorial design because there are two levels of one factor (drug) and two levels of a second factor (task description). The first number in the notation for a factorial design refers to the number of levels of the first factor and the second number refers to the number of levels of the second factor. Thus, if Sally instead chose to study four dosages of the drug and three values of task description, then she would be using a 4 x 3 factorial design. She might also choose to include yet another factor (C) in the same experiment; perhaps she tells subjects either that the drug is expected to impede their memory (C1) or that it is expected to enhance their memory (C2). If her design consisted of three factors with two levels each, then she would be using a 2 x 2 x 2 factorial design.
Factorial designs allow researchers to more closely approximate the complexities of the real world, where it is unlikely that one independent variable works in isolation from all others. Suppose Sally did not employ a factorial design; instead, she ran two experiments to separately assess the effects of drug dosage and task description on memory. In Experiment 1, to control for task description, she holds it constant and varies drug dosage. She might choose to tell subjects nothing about the task difficulty and simply manipulate whether or not the pill contains the drug. In Experiment 2, to control for drug dosage, she holds it constant and varies the task description. She might choose to always administer the drug and manipulate whether or not she tells subjects that the task is "hard." Table 2 and Table 3 below outline these two experiments.
| DRUG DOSAGE (A) at B1 | TASK DESCRIPTION (B) at A2 | ||||||
| 0 mg (A1) | 10 mg (A2) | None (B1) | "Hard" (B2) | ||||
|
|
||||||
| TABLE 2. Outline of an experiment in which two levels of drug dosage are varied at one level of task description. | TABLE 3. Outline of an experiment in which two levels of task description are varied at one level of drug dosage. | ||||||
Note that Sally's conclusion about the effect of the independent variable in each experiment would be restricted to the level of the other variable under which it was studied. As we will see, a major advantage of the factorial design is that it is an efficient way of exploring whether or not interdependencies between two or more independent variables exist.
We should mention one other major advantage of the factorial design. Reconsider the experiment outlined in Table 2 above. Suppose Sally suspects that certain subjects will be predisposed to believe that the task is a difficult one. Should the number of subjects with this belief be unequally represented in the two drug dosage conditions and the memory task scores differ between those conditions, she would be unable to conclude whether the drug or the belief was the causal variable. However, she is confident that by randomly assigning subjects to the two drug dosage conditions the number of subjects with this belief will be evenly distributed and the outcome will not be confounded by this variable. (To learn more about selection as a confounding variable, click here.) The factorial design goes one step further: it not only controls for the "belief" variable, it also tells how much of an effect that variable has in that situation. It controls for the belief variable by intentionally distributing it among the conditions unevenly. (Presumably more subjects exposed to the condition in which the task is described as "hard" will believe that to be true than subjects who are given no task description.) Nothing is left to chance in this regard. Sally can then ask: Do performances at one level of task description actually differ from those at the other level? Adding this extra factor to the experiment allows Sally to confirm or disconfirm her suspicion, in addition to assessing the effect of the drug. Should the drug be found to impede memory, she will be better able to specify the conditions under which it does so.