Factorial Designs: Special Considerations
Subject Assignment
As you are no doubt well aware by now, a factorial design contains multiple conditions. So, given a pool of subjects, which subject participates under which condition(s)? There are several possibilities. In a between-subjects design, subjects are randomly assigned to one of the conditions, each subject experiencing that one condition only. In our example, given a pool of 40 subjects, 10 subjects might participate under the no drug and no task description condition (A1B1), 10 other subjects under the no drug and "hard task" description condition (A1B2), 10 other subjects under the drug and no task description condition (A2B2), and 10 other subjects under the drug and "hard task" description condition (A2B2). In a within-subjects design, each subject experiences every one of the conditions. In our example, given a pool of 10 subjects, the same 10 subjects would participate under A1B1, and under A1B2, and under A2B1, and under A2B2. Note that fewer subjects are required in a within-subjects design.
Sometimes a mixture of these two designs is employed. In a 2 x 2 factorial design, subjects might be randomly assigned to one of the two levels of Factor B, and experience both levels of Factor A. In our example, Sally may have a pool of 20 subjects and the experiment may consist of two sessions. For 10 subjects, there is no task description in either session; in addition, in one session these subjects do not take the drug (A1B1) and in the other session they do take it (A2B1). For 10 other subjects, a "hard" task description is provided in both sessions, one session without the drug (A1B2) and the other with the drug (A2B2). Sally might employ this design if she suspects a carry-over effect with regards to task description, e.g., telling subjects in the first session that the task is "hard" may lead them to believe the task is hard in the second session even though it is not described as such. Carry-over effects are a potential problem in within-subjects designs.
Finally, assignment to the levels of one factor may be fixed in advance, based upon a set characteristic that subjects bring into the experiment. For example, Factor B in our example could be the gender of the subject. Note that subjects cannot be randomly assigned to one of the two levels (male or female) of this factor. This arrangement, in which one of the factors cannot be manipulated by the experimenter, is called a quasi-factorial design. If neither factor can be manipulated (e.g., gender and age), then the arrangement is called a factorial ex post facto design (Sowell & Casey, 1982). When random assignment to levels of an independent variable is not employed, selection poses a threat to internal validity; one needs to be very cautious in interpreting a causal relationship between that independent variable and the dependent variable. (To learn more about selection as a confounding variable, click here.)
Each of the aforementioned designs has its uses in psychological research, with its own unique advantages and limitations. The reader is encouraged to consult a textbook in research methods to learn more about this topic (e.g., McBurney, 2004).
Levels and Factors
Earlier we mentioned that a factorial design could include more than two factors and any given factor could include more than two levels. Figure 4 below extends our example to a 3 x 2 factorial design. Sally's experiment now includes three levels of the drug: 0 mg (A1); 5 mg (A2); and 10 mg (A3).
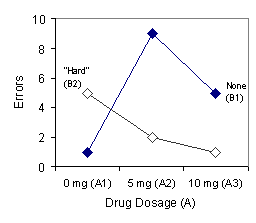
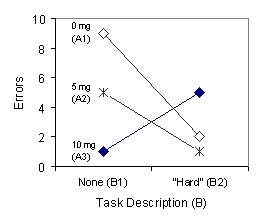
FIGURE 4. Graph illustrating an interaction between Factor A and Factor B in a 3 x 2 factorial design.
The lines in each graph are not parallel, so an interaction is taking place. How might you describe it? As you can see, data interpretation becomes considerably more complex by adding only one more level of one factor.
Suppose instead that Sally decides to include an additional factor in her experiment, such as subject gender. We can think of this design in terms of two separate tables, one for males and one for females, as outlined in Table 7 below.
| MALES (C1) | TASK DESCRIPTION (B) | ||||||
| None (B1) | "Hard" (B2) | ||||||
| DRUG DOSAGE (A) | 0 mg (A1) |
|
|||||
| 10 mg (A2) | |||||||
| FEMALES (C2) | TASK DESCRIPTION (B) | ||||||
| None (B1) | "Hard" (B2) | ||||||
| DRUG DOSAGE (A) | 0 mg (A1) |
|
|||||
| 10 mg (A2) | |||||||
Here is what Sally would need to consider when analyzing her data:
- A main effect for Factor A (e.g., does the drug affect memory?)
- A main effect for Factor B (e.g., does the task description affect memory?)
- A main effect for Factor C (e.g., does gender affect memory?)
- An interaction between Factor A and Factor B (e.g., is the nature of the relationship across both levels of the drug different when there is no task description than when the task is described as "hard"?)
- An interaction between Factor A and Factor C (e.g., is the nature of the relationship across both levels of the drug different when the subject is male than when the subject is female?)
- An interaction between Factor B and Factor C (e.g., is the nature of the relationship across both levels of the task description different when the subject is male than when the subject is female)
- An interaction between Factor A and Factor B and Factor C (e.g., is the nature of the interaction between the drug and the task description different when the subject is male than when the subject is female?)
Is there a limit to the number of factors and levels of each factor? To this question McBurney (2004) replies:
"Of course, you can have as many factors and levels as you desire, but with increasing complexity you will require much more time to conduct the experiment. In addition, considering large number of interactions taxes the mind, defeating the purpose of doing the experiment in the first place. Most experiments use two to three factors, with two to six levels on the various factors." (p. 287).